Resolución De Ecuaciones
Resolver una ecuación es hallar su solución o soluciones, o bien concluir que no tiene solución. Para resolver una ecuación, se pasa a otra equivalente cuya fisonomía es más sencilla. Para averiguar el valor de x debe despejarse la letra incógnita. Para ello nos valemos de una propiedad matemática (propiedad uniforme) que nos permite poner un mismo número en ambos miembros de la expresión algebraica, siempre y cuando se mantenga la igualdad.
4x - 7 + 7 = 1 + 7 (por eso se dice que un numero que está restando "pasa" sumando).
4x = 1 + 7
4x = 8
4x : 4 = 8 : 4 (por eso se dice que un numero que está multiplicando "pasa" dividiendo)
Tiene una única solución: x = 2.
Sin embargo, hay tipos de ecuaciones para cuya resolución se requieren técnicas especiales. Es el caso, por ejemplo, de las ecuaciones cuadráticas y bicuadradas.
Resolución de ecuaciones cuadráticas
No existe una única forma de escribir la ecuación cuadrática.
La forma canónica: f(x) = a (x - vx)2 + vy [donde (-vx ; vy) es la coordenada del vértice de la parábola]
La expresión polinómica f(x) = ax2 + bx + c representan diferentes formas de expresar la misma función. Veamos como se pasa de una a otra.
- Las ecuaciones de segundo grado de los tipos siguientes se llaman incompletas porque les falta uno de los términos:
ax2 + bx = 0
ax2 + c = 0Se pueden resolver aplicando la fórmula general, pero es más cómodo resolverlas despejando directamente la x.
En el primer caso,
ax2 + bx = 0 ! (ax + b)x = 0
Una solución es x = 0 y la otra se obtiene resolviendo la ecuación lineal ax + b = 0. Por ejemplo:
3x2 + 5x = 0 ! (3x + 5)x = 0
Las soluciones son: x = 0; x = - 5/3.
En el segundo caso,
ax2 + c = 0 ! ax2 = - c ! x2 = - c/a
- Resolución de ecuaciones bicuadradas:
Se llama bicuadrada a una ecuación polinómica de cuarto grado que no tiene términos de grado impar:
ax4 + bx2 + c = 0 (1)Si se realiza el cambio de variable x2 = z, con lo cual x4 = z2, entonces se transforma en una ecuación de segundo grado:
az2 + bz + c = 0 (2)
Sistemas de ecuaciones
Llamamos sistema de ecuaciones a un conjunto cualquiera de ecuaciones. Por ejemplo, las ecuaciones:
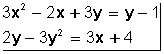
forman un sistema de dos ecuaciones con dos incógnitas.
El conjunto de ecuaciones:
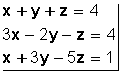
forman un sistema de tres ecuaciones con tres incógnitas.
Se llama grado del sistema de ecuaciones al mayor exponente al que se encuentre elevada alguna incógnita del sistema.
Por ejemplo,
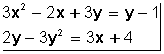
es un sistema de dos ecuaciones con dos incógnitas de segundo grado, porque el mayor exponente es 2 (la x e y al cuadrado). Este sistema con ecuaciones de segundo grado se llaman también sistema de ecuaciones cuadráticas.
El sistema de ecuaciones
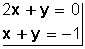es de primer grado con dos incógnitas (porque todos los valores están elevados a 1, que no se escribe).Cuando el sistema de ecuaciones es de primer grado y además no aparecen términos con las incógnitas multiplicadas entre sí (tipo x • y) se dice que es un sistema de ecuaciones lineales.
Resolviendo sistemas
Para resolver un sistema de ecuaciones existen los siguientes métodos:
- Método de sustitución
Lo que debemos hacer:
1.- Despejar una de las incógnitas en una de las ecuaciones.
2.- Sustituir la expresión obtenida en la otra ecuación.
3.- Resolver la ecuación resultante.
4.- Calcular la otra incógnita en la ecuación despejada.
Ejemplo:
Resolver
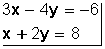
Se despeja x en la segunda ecuación:
x = 8 – 2y
Se sustituyen en la primera ecuación:
3(8 – 2y) – 4y = – 6
Operando:
24 − 6y − 4y = − 6
24 – 10y = – 6
− 10y = − 6 − 24
− 10y = − 30
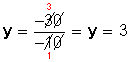
Se resuelve:
y = 3
Se sustituye este valor en la segunda:
x + 2(3) = 8
x + 6 = 8
x = 8 – 6 = 2
Solución del sistema:
x = 2, y = 3
- Método de reducción
Lo que debemos hacer:
1.- Se igualan los coeficientes de una incógnita, salvo el signo, eligiendo un múltiplo común de ambos.
2.- Puede ser el producto de los coeficientes de esa incógnita.
3.- Se suman o restan, según convenga, las ecuaciones.
4.- Se resuelve la ecuación de primer grado resultante.
5.- Se calcula la otra incógnita sustituyendo el valor obtenido en una de las ecuaciones del sistema.
Ejemplo:
Resolver
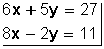
Primero se deben igualar el 6 y el 8 de la incógnita x. Para hacerlo, amplificamos la primera ecuación por 4 y amplificamos la segunda ecuación por –3. Esto porque al multiplicar 6x por 4 queda 24x; y al multiplicar 8x por –3 queda –24x, y se anulan entre sí; o sea, hemos eliminado una incógnita para trabajar solo con la otra (la y). Luego hacemos lo mismo con la y.
Se elimina la x: Se elimina la y:
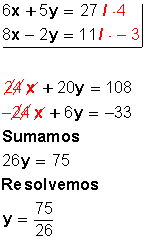
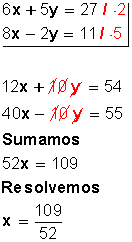
- Método de igualación
Lo que debemos hacer:
1.- Se despeja una de las incógnitas en ambas ecuaciones.
2.- Se igualan las expresiones, con lo que obtenemos una ecuación con una incógnita.
3.- Se resuelve la ecuación resultante.
4.- El valor obtenido se sustituye en cualquiera de las dos expresiones en las que aparecía despejada la otra incógnita.
5.- Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo:
Resolver
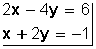
Despejamos x en la primera ecuación:
Despejamos x en la segunda ecuación:
x = –1 – 2y
Igualamos ambas expresiones:
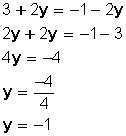
:Se sustituye este valor en la primera o segunda ecuación:
x = 3 + 2(−1)
x = 3 − 2
x = 1
Solución del sistema:
x = 1, y = –1
Otro ejemplo:
Resolver, por el método de igualación, el sistema
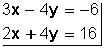
Despejamos, por ejemplo, la incógnita x de la primera y segunda ecuación:
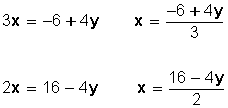
Igualamos ambas expresiones:
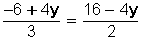
Luego, resolvemos la ecuación:
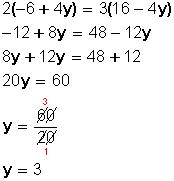
Sustituimos el valor de y, en una de las dos expresiones en las que tenemos despejada la x:
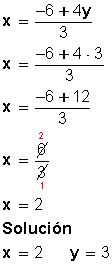
No hay comentarios:
Publicar un comentario